Regression
2024年12月23日大约 2 分钟
Regression
一元线性回归
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
X, Y = make_regression(n_samples=6,n_features=1,noise=3.5)
f(x) = coef_*x + intercept_
| 广告费 | 1.33997 | 0.34423 | 0.23107 | -0.84034 | -0.95766 | -2.28887 |
|---|---|---|---|---|---|---|
| 房价 | 36.21921 | -69.29114 | -20.52909 | 8.27876 | 8.45972 | -24.92423 |
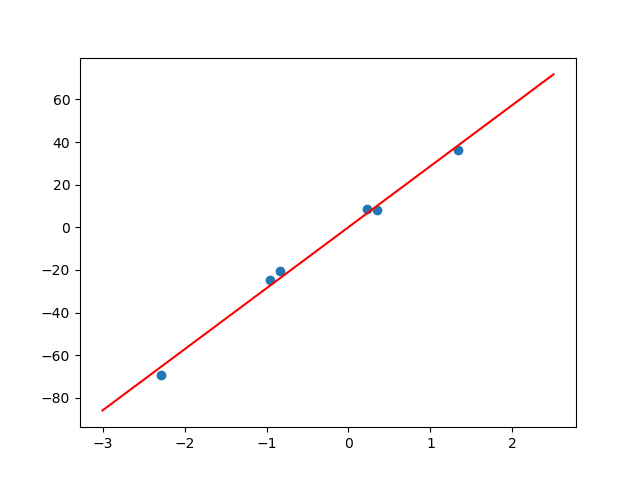
f(x) = coef_*x + intercept_
f(1.33997) = coef_*1.33997 + intercept_
f(0.34423) = coef_*(0.34423) + intercept_
f(0.23107) = coef_*(0.23107) + intercept_
f(-0.84034) = coef_*(-0.84034) + intercept_
f(-0.95766) = coef_*(-0.95766) + intercept_
f(-2.28887 ) = coef_*(-2.28887) + intercept_
(f(i) - (coef_*i + intercept_))^2 最小值
(coef_*1.33997 + intercept_ - 36.21921)^2
(coef_*0.34423 + intercept_ - (-69.29114))^2
(coef_*0.23107 + intercept_ - (-20.52909))^2
(coef_*(-0.84034) + intercept_ - 8.27876)^2
(coef_*(-0.95766) + intercept_ - 8.45972)^2
(coef_*(-2.28887) + intercept_ - (-24.92423))^2
S(coef_,intercept_) =
数学公式
from sympy import *
coef_ = Symbol('coef_')
intercept_ = Symbol('intercept_')
s = (coef_*1.33997 + intercept_ - 36.21921)**2 + (coef_*0.34423 + intercept_ - (-69.29114))**2 + (coef_*0.23107 + intercept_ - (-20.52909))**2 + (coef_*(-0.84034) + intercept_ - 8.27876)**2 + (coef_*(-0.95766) + intercept_ - 8.45972)**2 + (coef_*(-2.28887) + intercept_ - (-24.92423))**2
print(s.expand())
# 求偏导数
M = diff(s,coef_)
N = diff(s,intercept_)
print(M)
print(N)
M = 17.6592342136*coef_ - 4.3432*intercept_ - 123.8534451234
N = -4.3432*coef_ + 12.0*intercept_ + 123.57354
result = solve([M,N],[coef_,intercept_])
print(result)
{coef_: 4.91867087002977, intercept_: -8.51756405644056}
多元线性回归
- 影响房价因素
| 3.07671 | -0.07466 | -0.81435 |
|---|---|---|
| -0.81281 | 0.09361 | -0.20278 |
| -0.58860 | -1.30011 | -0.34815 |
| -1.56489 | 0.11505 | 0.02547 |
| 0.04549 | -0.05419 | 1.13453 |
| -0.66959 | -0.26893 | -1.18663 |
- 房价
| 54.76623 | -29.57975 | -54.72467 | -48.71732 | 50.02909 | -85.62378 |
|---|
数学公式
数学推导
- datasets
(x11,x12,x13,...,y11)
(x21,x22,x23,...,y12)
(x31,x32,x33,...,y13)
